Technical Library TEMPERAMENTS XXVI: Bach/Hill Entire Contents Copyright © 2021 CBH

American harpsichordist Robert Hill, now at University of Colorado Boulder College of Music but from 1990 to 2018 Professor of Historical Keyboard Instruments, Performance Practice & Chamber Music at the Freiburg Hochschule für Musik, discussed a different view of the Bach squiggle on his interesting blog Robert Hill Live in 2008.

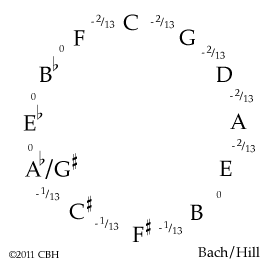
Of all the variations on this theme, Dr Hill’s interpretation is perhaps the most elegant. As we have seen, there are three kinds of circles in Bach’s squiggle: Empty, one loop and two loops. Most researchers—with the exception of David Louie—do not dispute that the empty circles represent pure fifths. Five circles on the right of the squiggle enclose double loops, three near the left end have single loops—this distinction most simply thought to refer to the two sizes of the tempered fifths, one with twice as much tempering as the other. All we have to worry about is where to start allocating pitches to the various circles in the squiggle. If we put A at the right and continue around the Circle of Fifths, the five double-looped fifths on the sharp side of F will be tempered twice as much as the three single-looped fifths from the sharp side of B, giving a very satisfactory result.

We can throw this distribution into our usual circular representation, and the similarity to many other so-called well temperaments can immediately be seen: The stronger-tempered fifths around C will again give better-sounding thirds in those much-needed keys. Interestingly, this layout preserves a pure fifth from e–b, like Bach/Barnes, Kellner or even Werckmeister III, slightly improving the more distant sharp keys even though the size of the tempered fifths differ between each of these temperaments.

For mathematical expediency to close the circle, here we require the basic tempered unit to be the rather strange size of a thirteenth-comma. Note, however, that from a practical point of view, there is probably very little audible difference between 2/13 comma and the familiar 1/6 comma of many other temperaments including Vallotti. If you agree with that, perhaps we can also accept the 1/13 comma fifth as near enough to the 1/12 comma of Equal Temperament. While our circle shows the two different physical sizes of tempered fifths, Dr Hill tunes his temperament by equal beats, making all five tempered fifths (double loops) beat about twice a second, and all three barely-tempered fifths (single loops) beat half that, at about once a second. This means, of course, that in practice each of his fifths higher up the keyboard are slightly less tempered and therefore proportionally smaller than their theoretical size shown as a uniform 2/13 comma here.

For instructions in how Dr Hill tunes this temperament from scratch, please refer to his blog entry.

If you have just tuned Vallotti, though, you can approximate the Bach/Hill temperament by changing only three pitches:

1. Raise your b to make a pure fifth above e.

2. The three fifths b–f♯', f♯–c♯' and c♯'–g♯' should be equally narrow, the single-loop error half the size of the tempered fifths made between most of the naturals. Tune a pure fifth b–f♯' and squeeze it slightly by lowering the f♯' until it beats about once per second. Compare the beat speed to the c'–g' fifth a semitone above. The latter is a double-loop, so should beat about twice the speed of your b–f♯'.

3. Do the same to c♯'–g♯' by raising the c♯' because you don’t want to move your already tuned g♯' of Vallotti. Make c♯'–g♯' beat with the same slow wave as b–f♯', again about once per second.

4. Tune down an octave from f♯' to f♯ and compare the resultant interval f♯–c♯'. If necessary, juggle these three single-loop fifths around to get them sounding with the same slow wave.

Dr Hill describes his version of the Bach temperament as “highly energized, but not over-wrought, and certainly not polarized in any way.” How do you find it?

	Pitch nomenclature
	Harpsichord Tuning Process
	Tuning Bibliography
	Technical Library overview
	Harpsichords Australia Home Page